阿里面试:全国14亿个姓名,统计出重名最多的前100个
全国14亿人的数据中,统计出重名人数最多的前100位姓名
最近有小伙伴在面试阿里,遇到这个面试题。小伙伴没有系统的去梳理和总结,所以支支吾吾的说了几句,面试官不满意,面试挂了。
TOP N面试题是常见的算法题。
TOP N 统计的面试题,是一道非常常见的题目,大家一定要掌握好。
1. 问题描述:
我们需要从全国14亿人的数据中,统计出重名人数最多的前100位姓名
2. 问题分析:
我们的目标:是找到重名人数最多的前100个姓名,
这意味着需要两步:
所以这个问题就转化成了下一个问题: 使用一种低成本、高性能的数据结构,来统计每个名字出现的次数。
3. 如何选择一种最低成本、最高性能的数据结构?
常规的数据结构,选型如下:
如果姓名的字符集范围很大(支持所有的Unicode字符),那么,需要极大且稀疏的数组,导致内存浪费严重,也不适合处理动态长度和多样性的字符串集合
跳表的插入、删除和查找操作的平均事件复杂度都是O(logN),
跳表式空间换时间的思想,主要是它需要额外的空间来维护多级索引,每个元素在最坏的情况下需要额外的存储空间,导致总的空间复杂度为O(N log N),
在频繁的插入和查询的场景中,效率不高。
来到我们现在这个场景,统计每个名字出现的次数时,不如哈希表在时间和空间的效率高效,哈希表的O(1)时间复杂度更适合大规模的数据频繁的插入和查询。
哈希表的插入和查找的时间复杂度都是O(1),
但是在极端的情况下,哈希冲突会导致时间复杂度退化到O(N),
在空间效率中,哈希表需要额外的空间来维护键值对,来到这个场景,空间效率和哈希冲突都有潜在风险,
最重要的是哈希表不能共享前缀,在处理大量的具有共同前缀的数据时候,也不适合。
能够维护有序数据,支持快速的插入、删除和查找操作,但在字符串的比较上,性能不如哈希表和Trie高效
前缀树通过共享前缀节点,节省了大量存储空间, 实现了成本的最低化
前缀树对于字符串操作非常高效, 在这个问题中, 有很多名字共享相同前缀, Trie的结构能有效利用这一特点。
经过上面的分析,能够看到Trie更适合统计每个名字出现的次数
4. 如何快速筛选出Top 100?
当知道了所有姓名出现的次数之后,、怎么样快速筛选出其中出现次数最多的前100个?
首先想到的是直接排序。
这个问题中,对14亿数据直接排序会有效率的问题,操作非常耗时。
所以直接排序, 这种方法不可取。
我们的目标是找到次数最多的前100个,可以利用堆的性质来完成。
小顶堆总是保持堆顶为当前堆中最小的元素,这样可以确保当新的元素插入时,如果新元素大于堆顶元素,堆顶元素会被替换掉
使用小顶堆的步骤:
1.初始化一个小顶堆:设为100
2.遍历每个姓名及其出现的次数:
3.遍历完所有的姓名后,堆中即为重名人数最多的前100个姓名
所以解决这个问题使用了前缀树 + 小顶堆
5. 前缀树Trie树介绍
在计算机科学中,trie,又称前缀树或字典树,使用一些单词来构建Trie树,如下图所示:
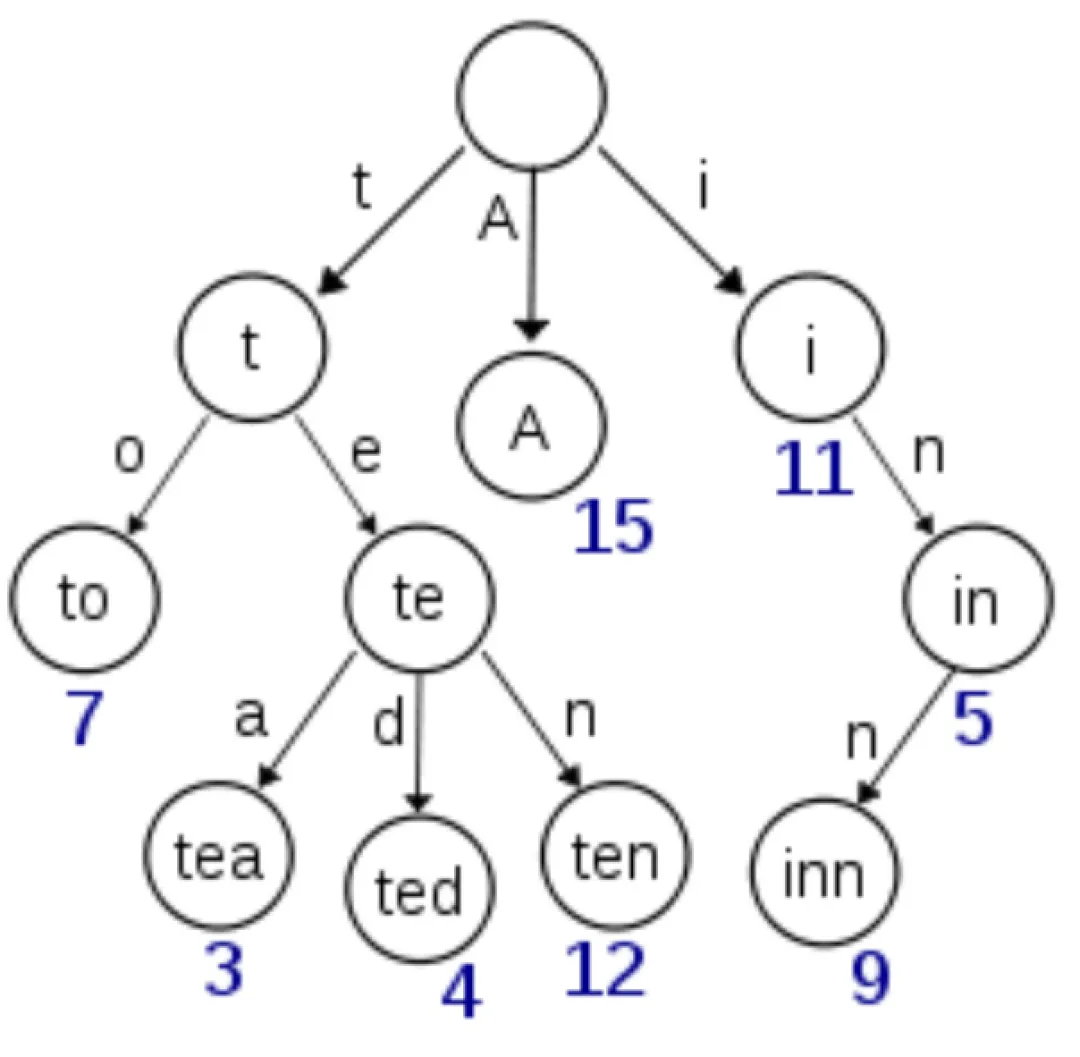
从图片中可以看到一些有意思的特性:
定义:
Trie树,又称为前缀树或字典树, 是一种用于高效存储和检索字符串集合的数据结构, 每个节点代表一个字符, 边表示从一个字符到另一个字符的路径, Trie树通过共享相同前缀的节点来节省存储空间
Trie树是一种有序树,用于保存关联数组,其中的键通常是字符串。
与二叉查找树不同,Trie树 的 键不是直接保存在节点中,而是由节点在树中的位置决定。
一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。
一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
trie中的键通常是字符串,但也可以是其它的结构。
trie的算法可以很容易地修改为处理其它结构的有序序列,比如一串数字或者形状的排列。
比如,bitwise trie中的键是一串位元,可以用于表示整数或者内存地址
Trie树基本性质
1,根节点不包含字符,除根节点意外每个节点只包含一个字符。
2,从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
3,每个节点的所有子节点包含的字符串不相同。
Trie树优点:
可以最大限度地减少无谓的字符串比较,故可以用于词频统计和大量字符串排序。
跟哈希表比较:
1,最坏情况时间复杂度比hash表好
2,没有冲突,除非一个key对应多个值(除key外的其他信息)
3,自带排序功能(类似Radix Sort),中序遍历trie可以得到排序。
Trie树缺点:
当所有关键字都不具有相同或类似的前缀,空间消耗过大.
6. Trie树的基本操作:
插入:将一个字符串逐字符插入到Trie树中
查找:检查Trie树中是否存在某个字符串
前缀匹配:查找所有以某个前缀开头的字符串
删除:从Trie树中删除一个字符串
7. Trie树的应用场景:
1.字符串检索:
2.自动补全:
3.前缀匹配:
应用场景:寻找以特定前缀开头的所有字符串,如电话号码前缀匹配
适用原因:Trie树天生适合处理前缀匹配问题,可以在O(L)时间内找到所有以特定前缀开头的字符串
4.词频统计:
为什么适合这些场景:
5.多模式匹配:
应用场景:从文本中同时搜索多个模式(模式匹配算法)
适用原因:Trie树可以构建多个模式的结构,通过一次遍历文本同时匹配多个模式,提高匹配效率
为什么适用于这些场景:
1.空间效率:
2.时间效率:
O(L)复杂度:插入、查找和前缀匹配操作的时间复杂度为O(L),其中L是字符串的长度,显著提高了操作效率
快速检索:相比于其他线性结构(如数组或链表),Trie树在处理大量字符串时更快
8. Trie树的代码实现:
以下是一个 参考代码:
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class TrieNode {
Map<Character, TrieNode> children;
int count;
public TrieNode() {
children = new HashMap<>();
count = 0;
}
}
class Trie {
private TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String name) {
TrieNode node = root;
for (char ch : name.toCharArray()) {
node = node.children.computeIfAbsent(ch, k -> new TrieNode());
}
node.count++;
}
public void getAllNames(TrieNode node, StringBuilder prefix, PriorityQueue<NameCount> minHeap, int k) {
if (node == null) return;
if (node.count > 0) {
if (minHeap.size() < k) {
minHeap.offer(new NameCount(prefix.toString(), node.count));
} else if (node.count > minHeap.peek().count) {
minHeap.poll();
minHeap.offer(new NameCount(prefix.toString(), node.count));
}
}
for (Map.Entry<Character, TrieNode> entry : node.children.entrySet()) {
prefix.append(entry.getKey());
getAllNames(entry.getValue(), prefix, minHeap, k);
prefix.deleteCharAt(prefix.length() - 1);
}
}
public PriorityQueue<NameCount> getTopKNames(int k) {
PriorityQueue<NameCount> minHeap = new PriorityQueue<>(k);
getAllNames(root, new StringBuilder(), minHeap, k);
return minHeap;
}
}
class NameCount implements Comparable<NameCount\> {
String name;
int count;
public NameCount(String name, int count) {
this.name = name;
this.count = count;
}
@Override
public int compareTo(NameCount other) {
return Integer.compare(this.count, other.count);
}
@Override
public String toString() {
return name + ": " + count;
}
}
public class Main {
public static void main(String\[\] args) {
String\[\] names = {"张伟", "王伟伟", "王芳", "李伟", "李娜"}; // 示例数据
int k = 100; // 找到前100个重名人数最多的姓名
Trie trie = new Trie();
for (String name : names) {
trie.insert(name);
}
PriorityQueue<NameCount> topKNames = trie.getTopKNames(k);
while (!topKNames.isEmpty()) {
System.out.println(topKNames.poll());
}
}
}
|
9. TOP N问题发散:
上面的问题进行改进一下, 如果我们对内存有一个限制,比如:要求内存的使用不能超过2G,
注意,这里的内存受限,尽量使用磁盘处理。
这里使用hashmap,而不适用 trie树的原因是?
trie树是按照字符为粒度组织树的节点的,进行磁盘操作性能不高,而且进行磁盘操作时算法更加复杂。
hashmap 是以key为单位操作的, 磁盘操作的效率高。而且 hashmap 统计的时候,代码简洁清晰。
尽管我们hashmap,也不能直接将所有数据加载到内存中处理,
所以可以采取分治的策略,使用外部排序和哈希映射的方法,
以下是详细的步骤:
1.分块读取数据:将14亿条记录分成多个较小的块,每次读取一部分数据到内存中进行处理
2.哈希映射统计词频:对每个块的数据进行哈希映射,统计每个名字出现的次数,将结果写入到磁盘文件
3.合并词频统计结果:读取所有中间文件,合并词频统计结果,得到全局的词频统计
4.使用小顶堆找出前100个重复最多的名字
import java.io.\*;
import java.util.HashMap;
import java.util.Map;
import java.util.PriorityQueue;
class NameCount implements Comparable<NameCount\> {
String name;
int count;
public NameCount(String name, int count) {
this.name = name;
this.count = count;
}
@Override
public int compareTo(NameCount other) {
return Integer.compare(this.count, other.count);
}
@Override
public String toString() {
return name + ": " + count;
}
}
public class ExternalMemoryTopK {
private static final int CHUNK\_SIZE = 1000000; // 每个块处理100万条记录
public static void main(String\[\] args) throws IOException {
String inputFile = "names.txt";
String outputFile = "top100names.txt";
int k = 100;
// 第一步:分块读取数据并统计词频
int chunkIndex = 0;
BufferedReader reader = new BufferedReader(new FileReader(inputFile));
String line;
while ((line = reader.readLine()) != null) {
Map<String, Integer> frequencyMap = new HashMap<>();
int lineCount = 0;
while (line != null && lineCount < CHUNK\_SIZE) {
frequencyMap.put(line, frequencyMap.getOrDefault(line, 0) + 1);
line = reader.readLine();
lineCount++;
}
writeFrequencyMapToFile(frequencyMap, "chunk\_" + chunkIndex + ".txt");
chunkIndex++;
}
reader.close();
// 第二步:合并所有块的词频统计结果
Map<String, Integer> globalFrequencyMap = new HashMap<>();
for (int i = 0; i < chunkIndex; i++) {
mergeFrequencyMapFromFile(globalFrequencyMap, "chunk\_" + i + ".txt");
}
// 第三步:使用小顶堆找出前100个重复最多的名字
PriorityQueue<NameCount> minHeap = new PriorityQueue<>(k);
for (Map.Entry<String, Integer> entry : globalFrequencyMap.entrySet()) {
if (minHeap.size() < k) {
minHeap.offer(new NameCount(entry.getKey(), entry.getValue()));
} else if (entry.getValue() > minHeap.peek().count) {
minHeap.poll();
minHeap.offer(new NameCount(entry.getKey(), entry.getValue()));
}
}
// 输出结果
BufferedWriter writer = new BufferedWriter(new FileWriter(outputFile));
while (!minHeap.isEmpty()) {
writer.write(minHeap.poll().toString());
writer.newLine();
}
writer.close();
}
private static void writeFrequencyMapToFile(Map<String, Integer> frequencyMap, String filename) throws IOException {
BufferedWriter writer = new BufferedWriter(new FileWriter(filename));
for (Map.Entry<String, Integer> entry : frequencyMap.entrySet()) {
writer.write(entry.getKey() + " " + entry.getValue());
writer.newLine();
}
writer.close();
}
private static void mergeFrequencyMapFromFile(Map<String, Integer> globalFrequencyMap, String filename) throws IOException {
BufferedReader reader = new BufferedReader(new FileReader(filename));
String line;
while ((line = reader.readLine()) != null) {
String\[\] parts = line.split(" ");
String name = parts\[0\];
int count = Integer.parseInt(parts\[1\]);
globalFrequencyMap.put(name, globalFrequencyMap.getOrDefault(name, 0) + count);
}
reader.close();
}
}
|
10. topK问题,典型的解题思路
这是一种典型的topK问题,一般的问法如下:
从一堆数据中选出多少个最大或最小数?
解题思想:
先统计数量, 使用前缀树,hashmap等
再用小顶堆或者 大顶堆
取大用小,取小用大。简单来说就是取最大的K个数就用小顶堆,取最小的K个数,就用大顶堆
取海量数据里面最小的K个数?
要找出数组中最小的K个数,就要构造一个有K个元素的大顶堆,因为大顶堆的堆顶值是最大的,其它元素和堆顶的元素比较,大于堆顶的元素,换一个元素继续,小于堆顶的元素,将堆顶元素出堆,将更小的元素插入堆顶,如此反复,堆里面就是最小的数
取海量数据里面最大的K个数?
要找出数组中最大的K个数,就要构造一个有K个元素的小顶堆,因为小顶堆的堆顶值是最小的,其它元素和堆顶的元素比较,大于堆顶的元素,堆顶的元素出堆,将元素插入到小顶堆,将更大的元素换到堆中,如此反复,堆里面就是最大的数




